| Sesión anterior | Volver a página principal | Siguiente sesión |
CURVAS QUE DEPENDEN DE ELEMENTOS MÉTRICOS
|
|
§ 1. Curvas en forma explícita
Son muchos los programas informáticos que permiten el trazado de curvas o superficies a partir de sus ecuaciones. En esta sección abordaremos cómo realizarlo con CABRI. No se tratará de un proceso inmediato puesto que hasta aquí se habrá podido apreciar que CABRI es un software especialmente dotado para el desarrollo de la geometría sintética. Sin embargo, utilizando las herramientas métricas y las transformaciones geométricas predefinidas (traslación, simetría, homotecia...) lograremos representar cualquier tipo de curva. Ahora nos ocuparemos de las curvas del tipo y = f(x). Aunque hay varios métodos para resolver la cuestión, el que se expondrá utiliza un número pequeño de rectas auxiliares.
Comenzaremos por mostrar un sistema de ejes coordenados con la herramienta Mostrar ejes. Nos interesa colocar puntos en las coordenadas (0,1) y (1,0) o, de modo equivalente, vectores unitarios con origen en O = (0,0) y extremos en las coordenadas anteriores que hagan de base del espacio vectorial real de dimensió 2. Para ello, activando la herramienta Definir cuadrícula, señalamos los ejes de forma que se sombrean todos los puntos del plano con coordenadas enteras. Esto proporcionará la precisión requerida para ubicar el punto U = (0,1). Sitúese un punto X sobre el eje de abscisas y un vector OX. Con la herramienta Ecuación y coordenadas, hallaremos las coordenadas (x,0) del punto X. Pongamos ahora la calculadora en funcionamiento. Traspasemos a ella la expresión f(x) a representar, donde cada ocurrencia de la variable x será sustituida por la abscisa x de X sin más que cliquear ésta con el ratón. Llevemos el resultado al tablero de trabajo. La homotecia de razón f(x) de centro O transforma el punto U en P, y la traslación de vector OX aplica P en el punto Y de coordenadas (x,f(x)). El Lugar geométrico que genera Y cuando X se desplaza por el eje de abscisas acaba la gráfica de la función y=f(x).
Figura 3.1
En la figura 3.1, está representada la curva
|
Ejercicio 3.1 Represéntese la curva de la figura 3.1.
Figura 3.2
De cualquier manera, hablando con rigor, en pantalla
no disponemos de la curva y = f(x),
sino de una aproximación de ella calculada por CABRI. Esto no supone inconveniente
para tratar tópicos de geometría diferencial. Por ejemplo,
supongamos que es nuestro deseo visualizar los vectores tangente y normal
en cada punto de la curva y = 2cos(x/2)
(figura 3.2), cuya derivada es y'
= -sin(x/2). Representada la función,
hallamos la imagen A de U
por la homotecia de centro O y razón
y'.
Consideremos los vectores
OA y OB
con B = (1,0). Es evidente que la suma de estos vectores
proporcionará el vector velocidad t
= t(x) a la curva. El giro de 90o
de t da un vector n
normal a la curva. Así se consigue trabajar con cualquier concepto
de la geometría diferencial relacionado con las curvas. Y también
nos está permitido ilustrar los procesos límite que dan lugar
a tales conceptos. Como muestra, en la figura 3.3
hay una aproximación del círculo osculador de la curva y
= 2cos(x/2). Veamos cómo se obtiene.
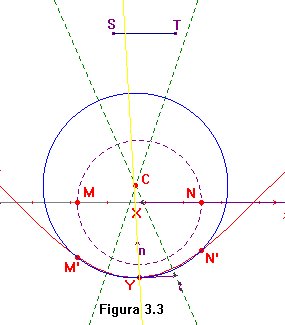 Recuérdese que el círculo osculador
de una curva en un punto es la circunferencia cuyo radio coincide con el radio de curvatura en
ese punto y cuyo centro
C = Y+(1/k)n
(donde k es la curvatura) se sitúa
sobre la recta normal. Dicho en términos clásicos, el círculo
osculador es una circunferencia que pasa por tres puntos
próximos.
Elijamos un segmento
ST lo suficientemente
grande, que nos servirá como radio de una circunferencia de centro
X
(en violeta en la figura). Sean M y
N
las intersecciones de esta circunferencia con el eje de abscisas. Con la
ayuda de una macro, a fin de economizar trazos, se han obtenido los puntos
M'
y N'
de la curva, que son las imágenes de M
y N por la correspondiente función.
La intersección de las mediatrices de los segmentos M'Y
y N'Y
dan el punto C, cercano al centro del
auténtico
círculo osculador. Bastará ahora con empequeñecer
el segmento ST para obtener una muy
buena aproximación del círculo osculador buscado.
Recuérdese que el círculo osculador
de una curva en un punto es la circunferencia cuyo radio coincide con el radio de curvatura en
ese punto y cuyo centro
C = Y+(1/k)n
(donde k es la curvatura) se sitúa
sobre la recta normal. Dicho en términos clásicos, el círculo
osculador es una circunferencia que pasa por tres puntos
próximos.
Elijamos un segmento
ST lo suficientemente
grande, que nos servirá como radio de una circunferencia de centro
X
(en violeta en la figura). Sean M y
N
las intersecciones de esta circunferencia con el eje de abscisas. Con la
ayuda de una macro, a fin de economizar trazos, se han obtenido los puntos
M'
y N'
de la curva, que son las imágenes de M
y N por la correspondiente función.
La intersección de las mediatrices de los segmentos M'Y
y N'Y
dan el punto C, cercano al centro del
auténtico
círculo osculador. Bastará ahora con empequeñecer
el segmento ST para obtener una muy
buena aproximación del círculo osculador buscado.
Ejercicio 3.2 Dada la curva y = 0.3 x2-2, represéntense los vectores tangente y normal y una aproximación del círculo osculador obtenida como circunferencia por tres puntos próximos.
§ 2. Elementos métricos en las cónicas
En la sesión II,
se realizó un estudio de las cónicas desde el punto de vista
de la geometría proyectiva, lo cual tiene la ventaja de que los
resultados allí descritos funcionan en planos sobre otros cuerpos
diferentes al de los números reales. Pero en el caso del plano euclídeo
las cónicas disfrutan de numerosas propiedades que involucran a
la métrica. La misma definición de cada una de las tres cónicas
no degeneradas puede darse en términos de la satisfacción
de determinadas propiedades métricas. Comencemos con la elipse.
Ésta se define como el lugar geométrico cuya suma de distancias
a
dos puntos dados, denominados focos,
es constante. 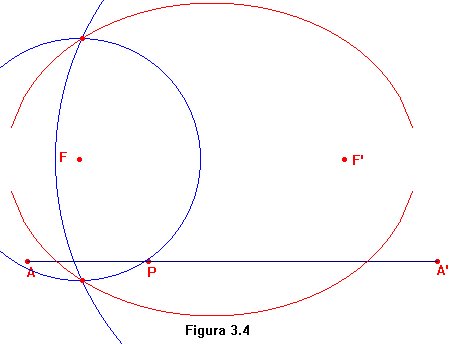 En
la figura 3.4 se ha representado una elipse utilizando esta característica.
Allí se parte de un par de puntos F
y F'
que harán el papel de focos, y de un segmento
AA'
cuya longitud es la suma de distancias que permanecerá constante.
Para un punto P situado sobre el segmento,
hemos trazado la circunferencia de centro F
y radio AP y la circunferencia de centro
F'
y radio A'P.
Los puntos donde se corten estas circunferencias han de pertenecer a la
elipse. Este proceso se conoce bajo el nombre de método
del jardinero.
En
la figura 3.4 se ha representado una elipse utilizando esta característica.
Allí se parte de un par de puntos F
y F'
que harán el papel de focos, y de un segmento
AA'
cuya longitud es la suma de distancias que permanecerá constante.
Para un punto P situado sobre el segmento,
hemos trazado la circunferencia de centro F
y radio AP y la circunferencia de centro
F'
y radio A'P.
Los puntos donde se corten estas circunferencias han de pertenecer a la
elipse. Este proceso se conoce bajo el nombre de método
del jardinero.
Ejercicio 3.3 Escríbase una macro tal que, sin más que señalar un segmento AA' y uno de los puntos F del segmento, dibuje una elipse con foco F y vértices A y A' en el eje mayor.
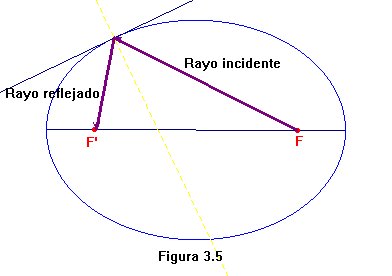
Las propiedades métricas de la elipse pueden ser simuladas con CABRI. Por ejemplo, es conocido que si una mesa de billar tiene forma elíptica y en uno de los focos se abre una tronera, entonces apuntando a cualquier punto de la banda desde el otro foco siempre conseguiremos introducir la bola en su agujero (véase la figura 3.5).
Ejercicio 3.4
Constrúyase una macro que trace la tangente a una elipse por un
punto y compruébese experimentalmente que los rayos que parten de
un foco pasan por el otro tras rebotar en la elipse. Recuérdense
las leyes de la reflexión.
 |
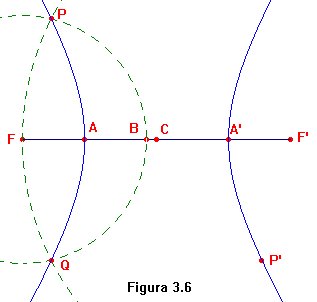 |
Ahora le toca el turno a la hipérbola. La definición euclídea de la hipérbola es parecida a la de la elipse, pero sustituyendo suma por diferencia. En concreto, una hipérbola es el lugar geométrico de los puntos cuya diferencia de distancias a dos dados (los focos) es constante. En la figura 3.6 se ilustra la construcción de una hipérbola de focos F y F' con vértice en A. El centro C de la hipérbola se ha obtenido como el punto medio entre los focos, y el otro vértice como el simétrico A' de A respecto a C. Sea B el simétrico de F respecto de A. Con centro en F y radio FB se ha trazado una circunferencia en trazo verde discontinuo. Hay otra circunferencia en el mismo trazo, la que tiene centro F' y radio FF'. El lector debería llegar a la conclusión de que los puntos de corte P y Q de ambas circunferencias pertenecen a la hipérbola. CABRI nos permite trazar una cónica sabiendo de ella cinco puntos. Hasta el momento solo conocemos cuatro: A, A', P y Q. Pero como el centro de una cónica con centro es un centro de simetría, basta hallar el simétrico P' de, por ejemplo, P, para disponer de los cinco puntos necesarios.
Ejercicio 3.5 Escríbase una macro que dibuje una hipérbola a partir de los focos y uno de los vértices.
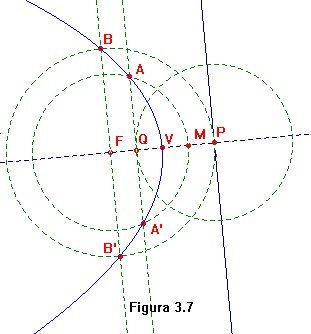 La
parábola también posee una definición métrica,
a saber, el lugar geométrico de los puntos equidistantes de una
recta, llamada directriz, y un punto
denominado foco. En la figura
3.7 se ha construido una parábola a partir del foco F
y la directriz. Sean P el pie de la
perpendicular por F a la directriz
y V el punto medio entre F
y P. Evidentemente V
pertenece a la parábola. Nos faltan otros cuatro para dibujar la
parábola. Para ello, si escogemos un punto Xen
el eje FP, trazamos por él una perpendicular
al eje y, por F, una circunferencia de
radio
d(X,P), los cortes
de esta circunferencia con aquella perpendicular darán más
puntos de la parábola. Tal proceso se ha seguido en la figura 3.7
a partir de los puntos medios M = [(V+P)/2]
y Q = [(V+F)/2].
La
parábola también posee una definición métrica,
a saber, el lugar geométrico de los puntos equidistantes de una
recta, llamada directriz, y un punto
denominado foco. En la figura
3.7 se ha construido una parábola a partir del foco F
y la directriz. Sean P el pie de la
perpendicular por F a la directriz
y V el punto medio entre F
y P. Evidentemente V
pertenece a la parábola. Nos faltan otros cuatro para dibujar la
parábola. Para ello, si escogemos un punto Xen
el eje FP, trazamos por él una perpendicular
al eje y, por F, una circunferencia de
radio
d(X,P), los cortes
de esta circunferencia con aquella perpendicular darán más
puntos de la parábola. Tal proceso se ha seguido en la figura 3.7
a partir de los puntos medios M = [(V+P)/2]
y Q = [(V+F)/2].
Ejercicio 3.6 Constrúyase una macro que dibuje una parábola dados su foco y su directriz.
Ejercicio 3.7 Compruébese experimentalmente el fundamento de los telescopios astronómicos basados en el sistema de espejos ideado por Newton, esto es, que los rayos paralelos al eje de una parábola convergen todos en su foco.
Y aunque cada una de las tres cónicas afines no degeneradas posee una definición métrica particular, hay una cualidad que las engloba a todas en el mismo saco. Para ello son precisos tres ingredientes, un punto llamado foco, una recta denominada directriz y un número real no negativo e conocido como excentricidad. Con tales elementos, se define una cónica como el lugar geométrico de los puntos cuyo cociente de distancias al foco y a la directriz permanece constantemente igual a la excentricidad. Resulta de cajón que la parábola no será sino la cónica de excentricidad e = 1. Excentricidades entre 0 y 1 darán elipses y para valores mayores que la unidad se obtienen hipérbolas. La cónica de excentricidad 0 se contrae hasta un punto, el foco (pareja de dos rectas imaginarias que se cortan en un vértice real), y si se permite hablar de la cónica de excentricidad infinita, esta se reduciría a la propia directriz (par de rectas superpuestas). El resto de los casos degenerados no caen dentro de esta definición.
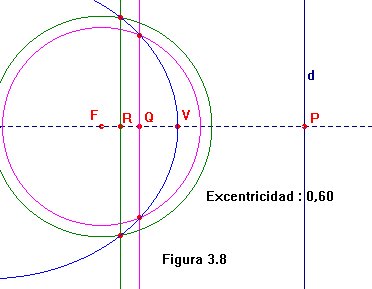
Abordemos la tarea de construir una cónica
de foco, directriz y excentricidad dadas (figura 3.8).
Con la calculadora, coloquemos la excentricidad,
0.60
en nuestro caso, en el tablero de trabajo. Si cliqueamos dos veces con
la herramienta Puntero en ese valor, podremos cambiar el texto del
mismo. Conviene titular los distintos resultados de la calculadora a fin
de evitar confusiones futuras. Sea P
el pie de la perpendicular por el foco F
a la directriz d. El vértice
V
se ha obtenido como el punto del segmento FP
cuyo cociente de distancias a F y a
P
coincide con la excentricidad, es decir, se ha resuelto el sistema de ecuaciones
|
||||||||||
|
Lo más cómodo en CABRI es trasladar la cantidad d(P,V) a la semirrecta con origen en P que pasa por F. Tras estas acciones, habremos trazado el vértice V de la cónica. Sea Q el punto medio entre F y V. Dibujemos la circunferencia de centro F y radio ed(P,Q). Las intersecciones de esta circunferencia con la perpendicular por Q a la recta FP (ambas en morado) dan dos puntos de la cónica. Repetimos este proceso con el punto R = [(Q+F)/2] (circunferencia y perpendicular en verde), y ya tenemos los cinco puntos precisos para trazar la cónica buscada.
Ejercicio 3.8 Con foco y directriz fijos, represéntese por medio de una animación a la familia de cónicas con excentricidades entre 0 y 2. Conviene escribirse una macro previa.
§ 3. Curvas en coordenadas polares
CABRI puede devolvernos la ecuación de uno de sus objetos en coordenadas polares. Sin embargo, en esta sección nos interesa el problema inverso, el de representar la gráfica de una curva expresada en coordenadas polares. Dependiendo del tipo de función, habremos de actuar de una u otra forma. Supongamos que queremos representar la función r = f(q) solo en el primer giro, es decir, con q en el intervalo [0o,360o]. Comenzaremos por dibujar una semirrecta con origen en el polo O que hará de semieje polar. Para cualquier rayo polar hemos de considerar el ángulo entre 0o y 360o que forma con el semieje polar. La herramienta Ángulo solo devuelve valores entre 0o y 180o cuando se le dan como parámetros tres puntos. Por eso hay que colocar primero la Marca de ángulo y señalar la marca.
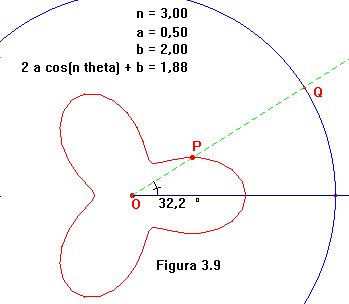 Pues bien, ilustraremos con un ejemplo cómo representar una curva
del tipo r
= 2 a cosnq +
b,
con n un número entero. En la
figura 3.9 está dibujado el caso n=3,
a=0.5, b=2.
Con la calculadora, llevamos los valores
n,
a
y b al tablero. Trazamos una circunferencia
con centro en el polo, un punto
Q sobre
ella y la semirrecta con origen en O
que pasa por Q (en trazo verde discontinuo).
Colocamos una marca de ángulo entre esta semirrecta, que hará
las veces de rayo polar, y el semieje polar, y lo medimos. Ahora evaluamos
2
a
cosnq
+
b y trasladamos esta distancia al rayo polar
para obtener el punto P de la curva.
Sin más que desplazar a Q sobre
la circunferencia, el punto P trazará
la curva pedida. La ventaja de haber colocado las variables en el tablero,
es que ahora podemos modificarlas a voluntad sin necesidad de cambiar la
ecuación. Supongamos por ejemplo que deseamos darle a n
y a b el valor 1.
Con la calculadora activa, cliqueemos dos veces sobre n
y recuperamos su valor. Lo cambiamos, y la curva se modifica automáticamente.
Haciendo
lo propio con b, se obtiene
la representación gráfica de r
= cosq+1, que no
es más que una de las cardioides de la sección
I § 7.
Pues bien, ilustraremos con un ejemplo cómo representar una curva
del tipo r
= 2 a cosnq +
b,
con n un número entero. En la
figura 3.9 está dibujado el caso n=3,
a=0.5, b=2.
Con la calculadora, llevamos los valores
n,
a
y b al tablero. Trazamos una circunferencia
con centro en el polo, un punto
Q sobre
ella y la semirrecta con origen en O
que pasa por Q (en trazo verde discontinuo).
Colocamos una marca de ángulo entre esta semirrecta, que hará
las veces de rayo polar, y el semieje polar, y lo medimos. Ahora evaluamos
2
a
cosnq
+
b y trasladamos esta distancia al rayo polar
para obtener el punto P de la curva.
Sin más que desplazar a Q sobre
la circunferencia, el punto P trazará
la curva pedida. La ventaja de haber colocado las variables en el tablero,
es que ahora podemos modificarlas a voluntad sin necesidad de cambiar la
ecuación. Supongamos por ejemplo que deseamos darle a n
y a b el valor 1.
Con la calculadora activa, cliqueemos dos veces sobre n
y recuperamos su valor. Lo cambiamos, y la curva se modifica automáticamente.
Haciendo
lo propio con b, se obtiene
la representación gráfica de r
= cosq+1, que no
es más que una de las cardioides de la sección
I § 7.
Ejercicio 3.9 Dibújese el folium de Descartes r = (4 a sin2q-b) cosq.
Otra problema se presenta si pretendemos trazar curvas en polares con un dominio superior al del primer giro, por ejemplo, una espiral logarítmica del tipo r = aebq. Aquí es mejor recurrir a las técnicas de la sección § 1 y situar un punto X sobre el eje de abscisas que nos servirá para medir ángulos. En la figura 3.10 se ha representado la espiral logarítmica r = e0.2q. Aquí, el punto Q no se desplaza libremente sobre la circunferencia, sino que es el resultado de girar A un total de q grados alrededor de O. Para ello se ha utilizado la herramienta Giro de CABRI. El resto del proceso es análogo al descrito más arriba.
Ejercicio 3.10 Represéntense la espiral de Arquímedes r = a q y la espiral hiperbólica r = 2/q.
§ 4. Curvas definidas por ecuaciones paramétricas
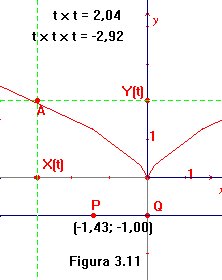 Tras lo visto en las secciones precedentes, no debería ser difícil
la representación de una curva
a(t)=(x(t),y(t))
dada por un par de funciones
x(t),
y(t)
que dependen de un parámetro
t.
Para dibujar, por ejemplo, a la parábola semicúbica
a(t)
= (t2,t3) (véase la figura
3.11), se ha trazado una recta por Q
paralela al eje de las equis y se ha situado en ella a un punto
P
cuya abscisa t actuará de parámetro.
Por medio de procesos ya conocidos, se has trasladado las longitudes
t2
y t3 a los semiejes positivos
de coordenadas para obtener los puntos X(t),
Y(t).
La intersección de la vertical por X(t)
con la horizontal por Y(t) describe
la curva
a.
Tras lo visto en las secciones precedentes, no debería ser difícil
la representación de una curva
a(t)=(x(t),y(t))
dada por un par de funciones
x(t),
y(t)
que dependen de un parámetro
t.
Para dibujar, por ejemplo, a la parábola semicúbica
a(t)
= (t2,t3) (véase la figura
3.11), se ha trazado una recta por Q
paralela al eje de las equis y se ha situado en ella a un punto
P
cuya abscisa t actuará de parámetro.
Por medio de procesos ya conocidos, se has trasladado las longitudes
t2
y t3 a los semiejes positivos
de coordenadas para obtener los puntos X(t),
Y(t).
La intersección de la vertical por X(t)
con la horizontal por Y(t) describe
la curva
a.
Ejercicio 3.11 Dése la representación gráfica de la curva
|
Si las componentes x(t) o y(t) de una curva a(t) = (x(t),y(t)) involucran a funciones trigonométricas y t representa un ángulo del primer giro, conviene utilizar a una circunferencia, en lugar de una recta, como campo de variación del parámetro. Por ejemplo, supongamos que es nuestro propósito representar la lemniscata de Bernoulli, que se define como el lugar geométrico de los puntos cuyo producto de distancias a dos fijos F y F', llamados focos es una cantidad constantemente igual a la cuarta parte del cuadrado la distancia entre los focos, esto es, descrito en términos conjuntistas,
|
No es difícil probar que si se sitúan los focos en los puntos de coordenadas F = (-f,0) y F' = (f,0), entonces la lemniscata queda descrita por la ecuación
|
|
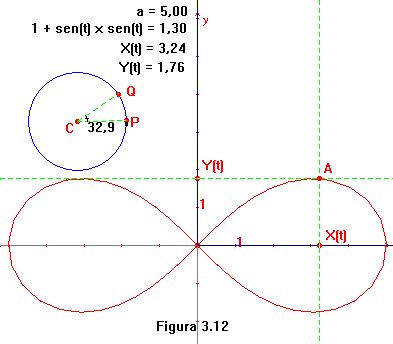 Ya disponemos de lo necesario para dar la representación gráfica
de la lemniscata de Bernoulli (sígase la figura
3.12). En una circunferencia de centro C,
fijemos un punto
P como origen de medida
de ángulos y situemos otro punto
Q
cuyo desplazamiento sobre la circunferencia provocará la variación
del parámetro t. Con la marca
de ángulo
PCQ obtendremos su
medida entre 0o y 360o.
Colocamos un valor a en el espacio
de trabajo por medio de la calculadora (en nuestro caso se ha dado un valor
inicial
a = 5). Ahora se procede como
antes fue descrito para evaluar las funciones componentes x(t),
y(t).
Al recorrer Q la
circunferencia, se traza la lemniscata completa.
Ya disponemos de lo necesario para dar la representación gráfica
de la lemniscata de Bernoulli (sígase la figura
3.12). En una circunferencia de centro C,
fijemos un punto
P como origen de medida
de ángulos y situemos otro punto
Q
cuyo desplazamiento sobre la circunferencia provocará la variación
del parámetro t. Con la marca
de ángulo
PCQ obtendremos su
medida entre 0o y 360o.
Colocamos un valor a en el espacio
de trabajo por medio de la calculadora (en nuestro caso se ha dado un valor
inicial
a = 5). Ahora se procede como
antes fue descrito para evaluar las funciones componentes x(t),
y(t).
Al recorrer Q la
circunferencia, se traza la lemniscata completa.
Ejercicio 3.12 Se define la astroide de grado n como la curva
Acabaremos esta sección tratando una familia
particularmente interesante de curvas: las curvas de Lissajous. Una curva
de Lissajous se obtiene físicamente como composición
de dos movimientos periódicos armónicos simples ortogonales
entre sí. En un caso práctico del mundo físico, supongamos
que a un péndulo que cuelga libremente y en reposo se le proporcionan
dos impulsos perpendiculares entre sí y a la cuerda. Cada una de
las proyecciones sobre los planos determinados por estas fuerzas y la posición
original de la cuerda se comportan como péndulos simples, pero el
resultado dibuja una curva de Lissajous. Estas gráficas aparecen
de forma natural en numerosos procesos físicos. En particular, son
las producidas por los osciloscopios. En la figura
3.13 hay representada una de estas curvas de Lissajous.
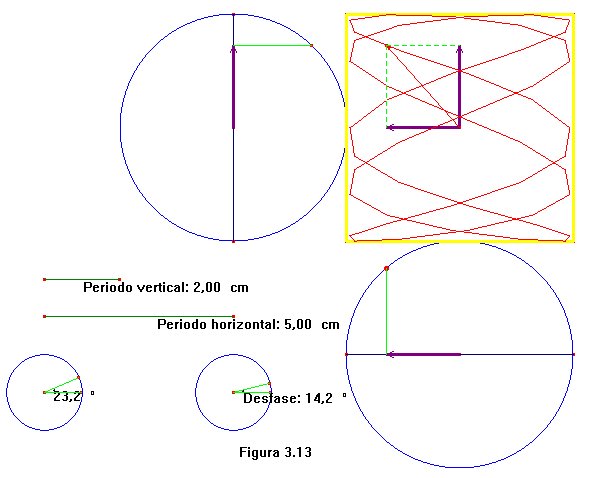 El parámetro varía al desplazarse un punto sobre la circunferencia más
pequeña de abajo a la izquierda. Que la proyección vertical
del movimiento tenga un periodo
2 significa
que por cada vuelta que complete el parámetro, el punto que hay
sobre la circunferencia mayor de arriba da 2
de ellas. La proyección de este punto sobre el diámetro vertical
define un vector (en violeta) cuyo extremo sigue un movimiento armónico
simple. De forma análoga, el la proyección horizontal del
movimiento posee un periodo 5, es decir, una
vuelta del parámetro produce cinco vueltas del punto que se desliza
sobre la mayor de las circunferencias de abajo. La proyección ortogonal
de este segundo punto sobre el diámetro horizontal determina un
segundo vector. La suma de ambos vectores es la que da la curva de Lissajous
representada. Adviértase que hay una tercera circunferencia pequeña
en la que se lee Desfase: 14.2o.
Esto significa que las componentes horizontal y vertical del movimiento
compuesto están desfasadas ese ángulo, en definitiva, que
la curva sigue una parametrización
El parámetro varía al desplazarse un punto sobre la circunferencia más
pequeña de abajo a la izquierda. Que la proyección vertical
del movimiento tenga un periodo
2 significa
que por cada vuelta que complete el parámetro, el punto que hay
sobre la circunferencia mayor de arriba da 2
de ellas. La proyección de este punto sobre el diámetro vertical
define un vector (en violeta) cuyo extremo sigue un movimiento armónico
simple. De forma análoga, el la proyección horizontal del
movimiento posee un periodo 5, es decir, una
vuelta del parámetro produce cinco vueltas del punto que se desliza
sobre la mayor de las circunferencias de abajo. La proyección ortogonal
de este segundo punto sobre el diámetro horizontal determina un
segundo vector. La suma de ambos vectores es la que da la curva de Lissajous
representada. Adviértase que hay una tercera circunferencia pequeña
en la que se lee Desfase: 14.2o.
Esto significa que las componentes horizontal y vertical del movimiento
compuesto están desfasadas ese ángulo, en definitiva, que
la curva sigue una parametrización
|
Además, en la figura se ha obligado a que los valores de los periodos (en principio 2 y 5) vengan en función de las longitudes de sendos segmentos que solo toman valores enteros. Para ello se ha recurrido a una cuadrícula que después ha sido ocultada. Así, sin más que modificar las longitudes de los segmentos, la curva de Lissajous se redibuja de modo automático. Una última dificultad se presenta para esta acción, y es que CABRI no puede mezclar unidades de distinta medida en los cálculos, o sea, se niega a sumar centímetros con grados o radianes con metros, por lo que es necesario eliminar la dimensión antes de procesar las cantidades 2cm y 5cm.
Ejercicio 3.13 Reprodúzcase el fichero CABRI de la figura 3.13.
Por curva de rodadura se entiende aquella que engendra un punto P ligado a una curva, denominada ruleta, cuando esta gira sin deslizarse sobre otra curva fija, llamada curva base, tangente a la anterior. En la figura 3.14 vemos un ejemplo de curva de rodadura. Allí, una circunferencia (ruleta) gira sin deslizarse sobre una recta tangente a ella (curva base). La curva que describe un punto de la circunferencia es una curva de rodadura.
 En este caso, en el que la ruleta es una circunferencia y la curva base,
una recta, a la curva de rodadura engendrada se le llama cicloide.
Pero el punto P puede también
adherirse solidariamente al exterior o al interior de la circunferencia,
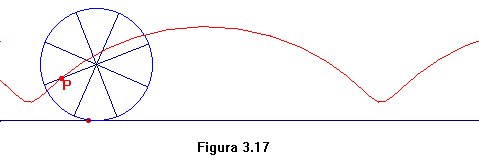
como se advierte en las figuras 3.16 y 3.17.
Puede comprobarse que en estos casos las curvas de rodadura generadas son
regulares, esto es, en cada punto hay una velocidad no nula (vector tangente
no nulo), mientras que en la cicloide de la figura 3.14, en el momento
en que el punto Ptoca el suelo, su
velocidad es cero puesto que en ese instante está adherido a él.
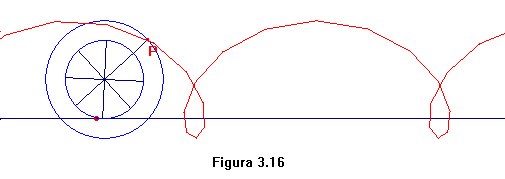
Aquella cicloide posee entonces puntos de singularidad. En la figura 3.16
podemos imaginarnos la simulación del movimiento de la parte más
externa de la rueda de un tren al desplazarse sobre los raíles.
De ahí que no se mienta al afirmar que cuando un ferrocarril avanza,
siempre hay partes de él que retroceden, que viajan en sentido contrario
al de la marcha.
En este caso, en el que la ruleta es una circunferencia y la curva base,
una recta, a la curva de rodadura engendrada se le llama cicloide.
Pero el punto P puede también
adherirse solidariamente al exterior o al interior de la circunferencia,
como se advierte en las figuras 3.16 y 3.17.
Puede comprobarse que en estos casos las curvas de rodadura generadas son
regulares, esto es, en cada punto hay una velocidad no nula (vector tangente
no nulo), mientras que en la cicloide de la figura 3.14, en el momento
en que el punto Ptoca el suelo, su
velocidad es cero puesto que en ese instante está adherido a él.
Aquella cicloide posee entonces puntos de singularidad. En la figura 3.16
podemos imaginarnos la simulación del movimiento de la parte más
externa de la rueda de un tren al desplazarse sobre los raíles.
De ahí que no se mienta al afirmar que cuando un ferrocarril avanza,
siempre hay partes de él que retroceden, que viajan en sentido contrario
al de la marcha.
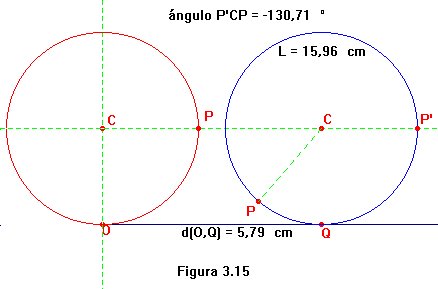
A continuación aprenderemos a construir mecanismos CABRI que reproduzcan esta familia de curvas de rodadura. Nos apoyaremos en la figura 3.15. En ella se representan la posición original de la circunferencia S (en rojo), y la posición final tras haber rodado un poquito sobre la recta r (en azul). El centro de la circunferencia se ha desplazado una longitud equivalente a la distancia d(O,Q) entre los dos puntos de tangencia. Para que S ruede sin deslizarse sobre la recta, el punto P ha debido de girar un ángulo P'CP, donde P' se encuentra en la posición original del punto P. Nuestro primer objetivo consistirá en determinar el valor de ese ángulo de giro. Para ello, hemos de comenzar observando que la distancia entre O y Q tiene que coincidir con la longitud del arco P'P pues, de lo contrario, la circunferencia habría derrapado. Una simple regla de 3 nos lleva al resultado pues,
|
|
Ejercicio 3.14
Constrúyanse mecanismos CABRI que generen las curvas de las figuras
3.14, 3.16 y 3.17.
 |
 |
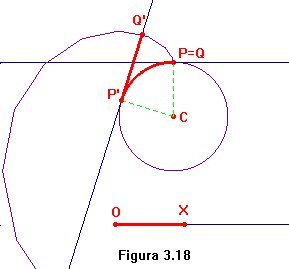 Ahora intercambiaremos los papeles de ruleta y curva base, es decir, la
curva base será una circunferencia, y la ruleta una recta tangente
a ella. A la curva de rodadura que engendra uno de los puntos de la recta
(figura 3.18) se le denomina evoluta de una circunferencia.
El primero en considerar estas curvas fue el matemático, físico
y astrónomo holandés Huygens, quien recurrió a ellas
estudiando los resortes que mueven a un reloj. En efecto, si nos imaginamos
que la recta representa a un fleje metálico enrollado en la circunferencia,
la curva que describe uno de sus puntos al soltarse el fleje y enderezarse
es una evoluta de circunferencia. Para obtener esta espiral
de Huygens, hemos utilizado una recta auxiliar que nos sirva
como medida de las longitudes. Y lo hemos hecho así porque CABRI
tiene ciertas limitaciones para operar con ángulos grandes. De esa
forma, sobre una semirrecta de origen O
hemos colocado un punto X. Consideramos
una recta tangente a la circunferencia en un punto P,
que se superpone al punto
Q de la recta.
cuando la recta gira sin deslizarse sobre la circunferencia y P
ocupa la posición
P',
el puntoQ se habrá movido hasta
Q'
dibujando parte de la espiral. Se trata entonces de trasladar la distancia
entre O y X
tanto a la recta como a la circunferencia. Con lo visto en párrafos
precedentes, ya hay suficientes pistas como para resolver sin problemas
el
Ahora intercambiaremos los papeles de ruleta y curva base, es decir, la
curva base será una circunferencia, y la ruleta una recta tangente
a ella. A la curva de rodadura que engendra uno de los puntos de la recta
(figura 3.18) se le denomina evoluta de una circunferencia.
El primero en considerar estas curvas fue el matemático, físico
y astrónomo holandés Huygens, quien recurrió a ellas
estudiando los resortes que mueven a un reloj. En efecto, si nos imaginamos
que la recta representa a un fleje metálico enrollado en la circunferencia,
la curva que describe uno de sus puntos al soltarse el fleje y enderezarse
es una evoluta de circunferencia. Para obtener esta espiral
de Huygens, hemos utilizado una recta auxiliar que nos sirva
como medida de las longitudes. Y lo hemos hecho así porque CABRI
tiene ciertas limitaciones para operar con ángulos grandes. De esa
forma, sobre una semirrecta de origen O
hemos colocado un punto X. Consideramos
una recta tangente a la circunferencia en un punto P,
que se superpone al punto
Q de la recta.
cuando la recta gira sin deslizarse sobre la circunferencia y P
ocupa la posición
P',
el puntoQ se habrá movido hasta
Q'
dibujando parte de la espiral. Se trata entonces de trasladar la distancia
entre O y X
tanto a la recta como a la circunferencia. Con lo visto en párrafos
precedentes, ya hay suficientes pistas como para resolver sin problemas
el
Ejercicio 3.15 Dibújese una espiral de Huygens.
En general, cuando la ruleta es una recta, a la curva de rodadura resultante se le denomina evoluta. Más concretamente, sea a(s)=(x(s),y(s)) una curva de velocidad unidad. Entonces, la evoluta de a es la curva b(s) = a(s)+sa'(s), es decir, es la curva que describe un punto de la recta tangente a a situado a una distancia s (la longitud de arco) del punto del tangencia. Físicamente esto es lo mismo que si la recta tangente se moviera sobre la curva sin deslizamiento. Si b es la evoluta de a, se dice de a que es la involuta de b. En cualquier libro de geometría diferencial elemental se demuestra que la evoluta de una curva es el lugar geométrico de los centros de los círculos osculadores de la curva. Así, un proceso como el descrito en la sección § 1 daría evolutas de curvas. Sin embargo, queremos terminar esta sección con un tópico distinto, el del trazado de la tractriz, aprovechándonos de un hecho bien conocido: La evoluta de una tractriz es una catenaria.
 Comenzaremos definiendo ambas curvas. La catenaria
es la curva con que se comba un cable de peso uniforme sometido a la gravedad.
Una catenaria simple queda descrita por la ecuación y
= coshx. Conviene entonces que vayamos definiendo macros
en CABRI que devuelvan el coseno y el seno hiperbólico de su entrada.
Por otro lado, una tractriz es una
curva con la propiedad de que existe una recta
r
tal que para cada punto de la curva, la distancia entre ese punto y la
intersección de la tangente con r se mantiene
constante. En términos físicos, si disponemos una barra rígida
y movemos uno de sus extremos por una recta ideal prependicular a la posición
original de la barra, el otro extremo describe una tractriz. Pues bien,
para obtener la tractriz como evoluta de la catenaria habrá que
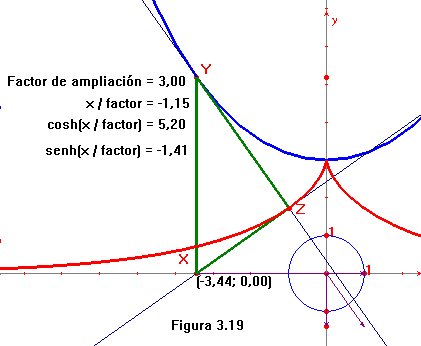
dibujar a esta primero (sígase la figura 3.19).
A fin de visualizar con mayor claridad, se ha utilizado un factor de ampliación
3,
lo cual significa que se aplica a todo el plano una homotecia de razón
3.
Así, si
Comenzaremos definiendo ambas curvas. La catenaria
es la curva con que se comba un cable de peso uniforme sometido a la gravedad.
Una catenaria simple queda descrita por la ecuación y
= coshx. Conviene entonces que vayamos definiendo macros
en CABRI que devuelvan el coseno y el seno hiperbólico de su entrada.
Por otro lado, una tractriz es una
curva con la propiedad de que existe una recta
r
tal que para cada punto de la curva, la distancia entre ese punto y la
intersección de la tangente con r se mantiene
constante. En términos físicos, si disponemos una barra rígida
y movemos uno de sus extremos por una recta ideal prependicular a la posición
original de la barra, el otro extremo describe una tractriz. Pues bien,
para obtener la tractriz como evoluta de la catenaria habrá que
dibujar a esta primero (sígase la figura 3.19).
A fin de visualizar con mayor claridad, se ha utilizado un factor de ampliación
3,
lo cual significa que se aplica a todo el plano una homotecia de razón
3.
Así, si
lo que nos lleva a la ecuación explícita y = 3 cosh(x/3). Con la ayuda de nuestra macro para el seno hiperbólico, hemos representado la recta tangente en Y. Pues bien, no es difícil demostrar que si trazamos por X la perpendicular s a la tangente, entonces s corta a la tangente en un punto Z cuya distancia a Y coincide con el valor 3sinh(x/3) de la longitud de arco entre el vértice de la catenaria y el punto Y. Disponemos entonces de un triángulo rectángulo de vértices X, Y y Z, de hipotenusa 3cosh(x/3), y uno de cuyos catetos vale 3sinh(x/3). La conocida relación entre las funciones hiperbólicas y el teorema de Pitágoras dan que la distancia d(X,Z) se mantiene constantemente igual a 3. Esto, unido a la ortogonalidad entre las tangentes en puntos homólogos de una curva y su evoluta acaban por probar que Z describe una tractriz.
Ejercicio 3.16 Constrúyase una tractriz como evoluta de una catenaria y compruébese empíricamente que esta es la involuta de aquella.
Estamos ahora en condiciones de obtener la evoluta de cualquier curva de la que podamos calcular sus tangentes y su longitud. Sin embargo, hay curvas cuya longitud de arco no es expresable en términos de funciones elementales. Por ejemplo, si queremos encontrar la longitud de arco de una elipse parametrizada por a(t) = (a cost, b sint), al intentar resolver la integral
|
 nos
topamos con una función no expresable en términos elementales
a menos que a = b. Pero podemos
hallar una aproximación de la longitud de arco gracias a CABRI.
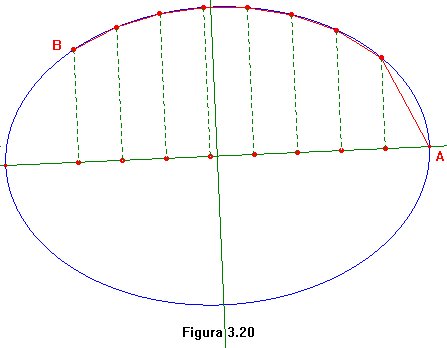
En la figura 3.20 hemos echado mano de la macro
del ejercicio 2.22 para obtener los
ejes y vértices de una elipse. Ahora, dado un punto
B
sobre la elipse, lo proyectamos ortogonalmente sobre el eje mayor y dividimos
el segmento determinado por esta proyección y el vértice
A
en un número de partes tan grande como queramos. Cuanto mayor sea
la partición, más preciso será el cálculo.
En nuestro caso lo hemos partido en
8 secciones
utilizando la herramienta
Punto medio. Cada uno de estos puntos
lo proyectamos ortogonalmente sobre la elipse y evaluamos la longitud de
la poligonal que va desde
A hasta B.
Esta cantidad proporciona una aproximación por defecto de la longitud
del arco de elipse entre
A y
B.
Una aproximación por exceso la proporcionaría la suma de
segmentos tangentes a la elipse en los puntos dados. La media aritmética
entre ambos valores da una razonable medida de la longitud del arco de
elipse AB.
nos
topamos con una función no expresable en términos elementales
a menos que a = b. Pero podemos
hallar una aproximación de la longitud de arco gracias a CABRI.
En la figura 3.20 hemos echado mano de la macro
del ejercicio 2.22 para obtener los
ejes y vértices de una elipse. Ahora, dado un punto
B
sobre la elipse, lo proyectamos ortogonalmente sobre el eje mayor y dividimos
el segmento determinado por esta proyección y el vértice
A
en un número de partes tan grande como queramos. Cuanto mayor sea
la partición, más preciso será el cálculo.
En nuestro caso lo hemos partido en
8 secciones
utilizando la herramienta
Punto medio. Cada uno de estos puntos
lo proyectamos ortogonalmente sobre la elipse y evaluamos la longitud de
la poligonal que va desde
A hasta B.
Esta cantidad proporciona una aproximación por defecto de la longitud
del arco de elipse entre
A y
B.
Una aproximación por exceso la proporcionaría la suma de
segmentos tangentes a la elipse en los puntos dados. La media aritmética
entre ambos valores da una razonable medida de la longitud del arco de
elipse AB.
Ejercicio 3.17 Obténgase una macro que de una aproximación de la longitud de una arco de elipse entre el vértice y un punto.
Ejercicio 3.18 Dibújese aproximadamente la evoluta de una elipse (figura 3.21).
§ 7. Trocoides y otros mecanismos
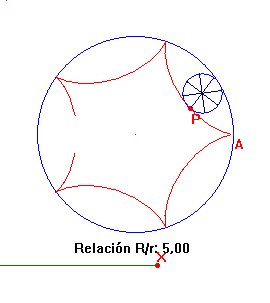
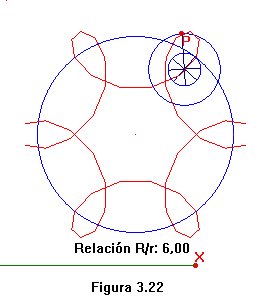
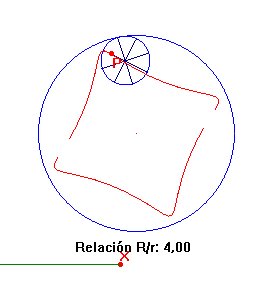
Una trocoide es una curva de rodadura en la que tanto la ruleta como la curva base son circunferencias. En la figura 3.22 hay representados varios tipos de trocoides. En los tres casos la ruleta es interior a la curva base. Se diferencian en la posición del punto que engendra la curva, interior a la ruleta, exterior o sobre ella. En los tres ficheros CABRI, la relación entre el radio de la curva base y el de la ruleta se ha expresado en función de la longitud de un segmento que solo toma valores enteros. Sin mayores indicaciones, el lector ha de ser capaz de resolver el
Ejercicio 3.19
Dibújense trocoides de ambos tipos, con la ruleta interior a la
curva base y con la ruleta exterior a la curva base.
 |
 |
 |
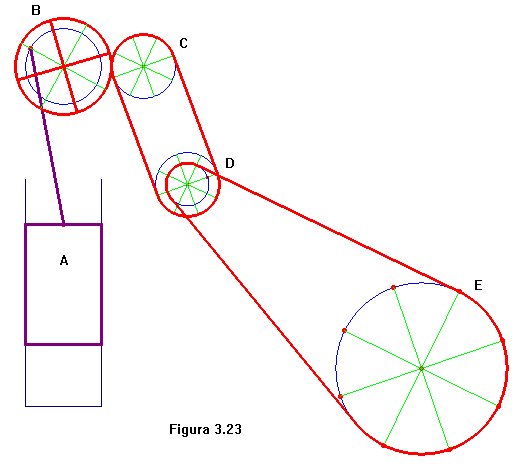 Todo lo visto en esta sesión resulta de utilidad a la hora de simular
mecanismos con CABRI. Por ejemplo, en la figura 3.23
un pistón
A mueve una rueda
B que embraga sobre otra C.
El movimiento circular se transmite hasta E
por medio de dos correas y una rueda reductora D.
Salvo el trazado de la correa que une D
con E, cualquiera de los demás
elementos puede ser dibujado con los conocimientos aprendidos hasta aquí.
Y para esta última circunstancia, solo hace falta encontrar las
tangentes comunes a dos circunferencias. A ello nos dedicamos en lo que
resta de capítulo.
Todo lo visto en esta sesión resulta de utilidad a la hora de simular
mecanismos con CABRI. Por ejemplo, en la figura 3.23
un pistón
A mueve una rueda
B que embraga sobre otra C.
El movimiento circular se transmite hasta E
por medio de dos correas y una rueda reductora D.
Salvo el trazado de la correa que une D
con E, cualquiera de los demás
elementos puede ser dibujado con los conocimientos aprendidos hasta aquí.
Y para esta última circunstancia, solo hace falta encontrar las
tangentes comunes a dos circunferencias. A ello nos dedicamos en lo que
resta de capítulo.
Dadas dos circunferencias de centros C y C', deseamos encontrar las tangentes comunes. Supongamos que el problema está resuelto y observemos la figura 3.24. Es evidente que el punto de corte de las tangentes comunes es el centro de una homotecia que transforma una circunferencia en otra. Bastará entonces hallar el centro de esa homotecia. Como las homotecias conservan el paralelismo, trácese cualquier radio CP a una de las circunferencias, y seaC'P' la paralela a CP por C'. La recta PP' ha de pasar por el centro de la homotecia, el cual también se encuentra sobre la recta que une los centros de las circunferencias.
Ejercicio 3.20 Simúlese un dispositivo mecánico animado con CABRI que contenga embragues, bielas y correas de transmisión entre ruedas de distinto radio. Si se desea, agréguense palancas, manivelas, levas o lo que dicte la imaginación.
| Sesión anterior | Volver a página principal | Siguiente sesión |