Sesión anterior	Volver a página principal	Siguiente sesión

§ 1. Proyectividades entre rectas del plano proyectivo real

    En toda esta sesión, se repasarán distintos conceptos de geometría proyectiva y se aprenderá a resolver ejercicios relacionados con tal parte de la matemática. En esta primera sección nos ceñiremos a las proyectividades entre rectas del plano proyectivo real. 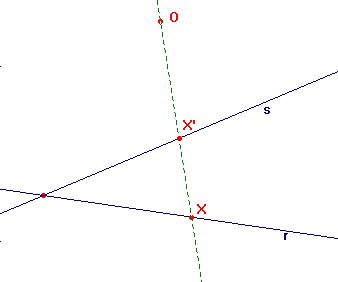Recuérdese que una proyectividad entre rectas del plano proyectivo real puede caracterizarse como una composición de perspectividades o como una biyección que conserva cuaternas armónicas. Por perspectividad de centro O entre las rectas r y s se entiende a la aplicación p_O:r->s que aplica cada punto X de r en el punto X' intersección de OX con r. (véase la figura 2.1). 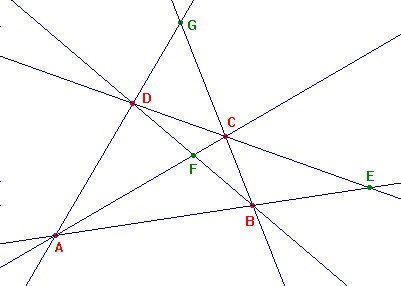Un cuadrivértice es una cuaterna de puntos (A,B,C,D)  sin tres de ellos alineados. Estos cuatro puntos, tomados de dos en dos, determinan seis rectas denominadas lados, las cuales se cortan en siete puntos, a saber, los cuatro vértices de partida y otros tres, E (intersección de AB con CD), F (intersección de AC con BD), y F (intersección de AD con BC), llamados puntos diagonales. En la figura 2.2 hay representado un cuadrivértice con sus tres puntos diagonales. 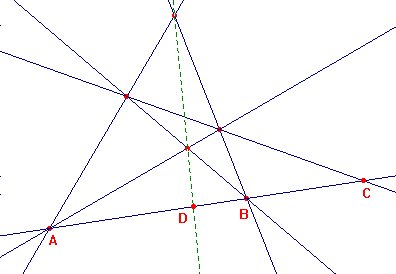De una cuaterna de puntos alineados (A,B,C,D) se dice que están en cuaterna armónica si hay un cuadrivértice del que A y B son vértices, C es uno de los puntos diagonales y D pertenece a la recta que pasa por los otros dos puntos diagonales. En la figura 2.3, los puntos A, B, C y D se encuentran en cuaterna armónica.
 

Figura 2.1	Figura 2.2

    Ejercicio 2.1 Dados tres puntos alineados distintos entre sí, constrúyase el cuarto armónico.
 
 

Figura 2.3	Figura 2.4

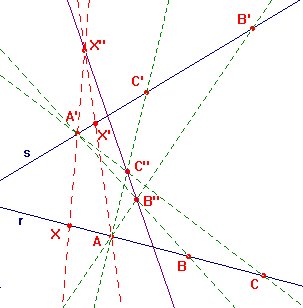
    El segundo teorema fundamental de la geometría proyectiva permite caracterizar una proyectividad entre rectas a partir de las imágenes de tan solo tres puntos. Para ello se procede de la siguiente forma: Dados A, B y C sobre una recta r y sus respectivas imágenes A', B' y C' por una proyectividad s:r->s, sean B" = AB'.A'B y C" = AC'.A'C (figura 2.4). Entonces la proyectividad s puede escribirse como la composición s = p_A°p_A' de la perspectividad p_A':r->B"C" de centro A' con la perspectividad p_A:B"C"->s de centro A. Así, la imagen X' = s(X) de un punto X de r, se obtendría como X' = AX".s, donde X" = A'X'.B"C".

    Ejercicio 2.2 Constrúyase una macro que proporcione la imagen X' de un punto X por una proyectividad s:r->s de la que se conocen las imágenes de tres puntos A, B y C de r.

    Cuando se trata de una proyectividad s de una recta r en sí misma, es necesaria una tercera perspectividad. En efecto, si s:r->r es una proyectividad que lleva A a A', B a B' yC a C', elíjanse una recta s distinta de r y un punto O fuera de las rectas r y s. Las rectas OA, OB y OC proporcionan intersecciones con s denotadas en la figura 2.5 por A1, B1 y C1 respectivamente. Ahora bastaría descomponer en producto de dos perspectividades a la proyectividad t:s->r que transforma A1 en A', B1 en B' y C1 en C'. Así, si quisiéramos hallar la imagen X' por s de un punto X perteneciente a r, sería suficiente con trazar el punto X1 perteneciente a s dado por X1 = OX.s y recurrir a la macro del ejercicio 2.2 para obtener la imagen t(X1) = s(X).

    Ejercicio 2.3 Dados tres puntos A, B y C sobre una recta r y sus respectivas imágenes A', B' y C' por una proyectividad s:r->r, trácese la imagen X' de cualquier otro punto X por esa proyectividad. Se permite recurrir a la macro construida en el ejercicio 2.2.

§ 2. Proyectividades en el plano

    Recuérdese que una proyectividad del plano proyectivo real no es sino una biyección que conserva puntos alineados. Además, como consecuencia del teorema fundamental de la geometría proyectiva, si s es una proyectividad del plano real y r es una recta, la restricción s|_r:r ->s(r) de dominio y recorrido de s resulta ser una proyectividad entre rectas del plano.

    Ciertas proyectividades del plano tienen un interés adicional que veremos en sesiones posteriores. Nos referimos a las homologías. Una homología es una proyectividad s del plano tal que hay un punto O, denominado centro, y una recta r denominada eje, tales que toda recta por O es doble (se aplica en sí misma) y todo punto de r es doble (se transforma en sí mismo). Dados el centro O y el eje r de una homología s, basta conocer la imagen P' de un punto P, con P distinto de O y P fuera de r, para averiguar el transformado X' de cualquier otro punto X. En efecto (véase la figura 2.6), la recta OX es doble, luego X' pertenece a OX, y la recta PX se transforma en la P'Q, donde Q = PX.r. Así, la imagen del punto X vendrá dada por X' = OX.P'Q.

    Ejercicio 2.4 Escríbase una macro que proporcione la imagen de un punto por una homología de la que se conocen el centro, el eje y el transformado de algún otro punto distinto del centro no perteneciente al eje.

    Del segundo teorema fundamental de la geometría proyectiva se desprende que una proyectividad del plano en sí misma queda determinada por la imagen de un cuadrivértice. Pongamos por caso que el cuadrivértice (A,B,C,D) se aplica en el cuadrivértice (A',B',C',D') por la proyectividad s (figura 2.7). Como las proyectividades conservan las relaciones de incidencia entre puntos y rectas, los puntos diagonales E, F y G del primer cuadrivértice han de transformarse en los puntos diagonales E', F' y G' del segundo. Como la restricción de dominio e imagen de s a una recta es una proyectividad entre rectas, la macro construida en el ejercicio 2.2 permite hallar la imagen de cualquier punto que se sitúe sobre los lados del primer cuadrivértice. Sea entonces X un punto que no pertenece a ninguno de los lados. Llamemos P a la intersección con el lado AB de la recta CX. Nuestra macro nos proporciona la imagen P' de P, luego X' = s(X) perteneciente a C'P'. Sea Q = AB.DX. De nuevo podemos calcular la imagen Q' de Q por s, y tendremos que X' pertenece a D'Q'. Luego X ha de aplicarse en X' = C'P'.D'Q'.

    Ejercicio 2.5 Constrúyase una macro que dé el transformado de cualquier punto del plano por una proyectividad de la cual se conocen las cuatro imágenes de los vértices de un cuadrivértice.

    Aprovecharemos ahora la macro del problema anterior para aprender a usar la herramienta CABRI redefinir objeto. En la figura 2.8, se han colocado nueve puntos en el tablero, los correspondientes a dos parejas de cuadrivértices (A,B,C,D) y (,A',B',C',D'), y un punto arbitrario X. Deseamos averiguar en quién se transforma una circunferencia por la proyectividad que aplica el primer cuadrivértice en el segundo. Pues bien, la macro del ejercicio 2.5 nos proporcionará la imagen X' del punto X por la proyectividad. Trazamos ahora la circunferencia y elegimos la herramienta Redefinir objeto. Señalando al punto X, se despliega un menú con varias opciones, la que nos interesa aquí es la Punto sobre objeto. Indicando la circunferencia con el ratón, el punto X pasa de ser un punto libre a un punto ligado a la circunferencia. Ahora basta con recurrir a Lugar geométrico para que se vea en qué curva se transforma la circunferencia.

    Ejercicio 2.6 Compruébese experimentalmente que la imagen de una cónica por una proyectividad es otra cónica.

§ 3. Proyectividades entre haces puntuales

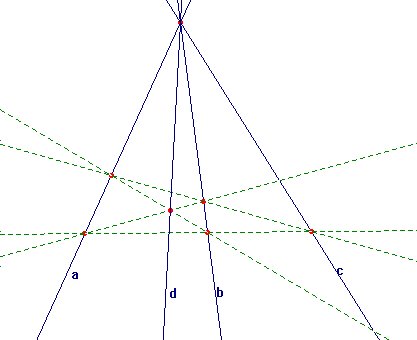
    El concepto dual de proyectividad entre rectas de un plano es el de proyectividad entre haces de rectas puntuales. En concreto, una biyección s:A^*->B^* entre el haz de rectas A^* que pasan por A y el haz de rectas B^* que pasan por B es una proyectividad entre haces puntuales, si conserva lápices armónicos. Un lápiz armónico es una cuaterna (a,b,c,d) de cuatro rectas concurrentes tales que a y b forman parte de los lados de un cuadrilátero del que c es una recta diagonal y d pasa por la intersección de las otras dos diagonales. En la figura 2.9 se encuentra trazado un lápiz armónico.
 
 

Figura 2.9	Figura 2.10

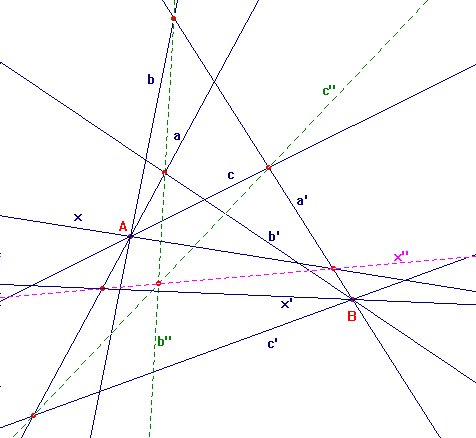
    Y al igual que sucedía con las proyectividades entre rectas, en este caso basta conocer la imagen de tres elementos para determinar una proyectividad entre haces puntuales. En efecto, supóngase que una proyectividad s:A^*->B^* entre haces aplica la recta a en la a', b en b' y c en c'. Sean b" la recta determinada por a.b' y a'.b, y c", la determinada por a.c' y a'.c (figura 2.10). Para cualquier otra recta x perteneciente a A^*, hágase x" la recta que pasa por b".c" y x.a'. La imagen de x por s será entonces la recta x' del haz B^* que pasa por a.x".

    Ejercicio 2.7 Escríbase una macro que dé la imagen de una recta x por una proyectividad entre haces puntuales de la que se conocen tres parejas de rectas homólogas.

    Ejercicio 2.8 Dada una proyectividad s:A^*->B^* entre haces puntuales, compruébese experimentalmente que el lugar geométrico de los puntos del tipo x.s(x), variando x en A^* es una cónica (figura 2.11). Este hecho fue aprovechado por Steiner para dar una definición sintética del concepto de cónica que no requiere de coordenadas ni de elementos métricos.

§ 4. Puntos dobles de una proyectividad

    Se verá más adelante que cuando s es una proyectividad entre un recta y ella misma o entre un haz puntual y él mismo cobran importancia los elementos que se aplican en sí mismos (puntos en el primer caso, rectas en el segundo), y que se adjetivan por medio de los términos doble o unido. Por ejemplo, si s:r->r es una proyectividad y P perteneciente a r satisface s(P) = P, entonces se dice de P que es un punto doble o un punto unido de s. Es un hecho conocido que, dada una proyectividad de una recta en sí misma o de un haz en él mismo distinta de la identidad, hay a lo sumo 2 elementos dobles. A continuación se describirá un método para encontrar los elementos unidos de una proyectividad basado en cierto teorema debido a Steiner.

    Supóngase que una proyectividad s de una recta r en sí misma transforma A en A', B en B' y C en C' (figura 2.12). Deseamos encontrar los puntos dobles, si los hubiere, de s. Para ello, trácese cualquier circunferencia S y elíjase en ella un punto O no perteneciente a r. Trasládense los tres puntos dados en r y sus imágenes a la circunferencia por medio de rectas que pasen por O para obtener los puntos A₁ = S.A, B₁ = S.B, C₁ = S.C, A'₁ = S.A', B'₁ = S.B' y C'₁ = S.C'. Sean U = A₁B'₁.A'₁B₁ y V = A₁C'₁.A'₁C₁. La recta UV, denominada eje de Steiner dirime la cuestión. Ella puede cortar a la circunferencia en 2, 1 ó 0 puntos dependiendo de si es secante, tangente o exterior. Pues bien, por cada intersección X del eje de Steiner UV con la circunferencia, se obtiene un punto doble para s, a saber, el punto OX.r. En el caso dibujado en la figura 2.12, hay un segundo punto doble que proviene de la otra intersección Y del eje de Steiner con la circunferencia.

    Ejercicio 2.9 Calcúlense los puntos dobles de una proyectividad s:r->r de la cual se conocen las imágenes de tres puntos.

    De forma análoga se procede para el cálculo de las rectas dobles de una proyectividad s:R^*->R^* de un haz puntual R^* en él mismo. Como datos, se conocen las imágenes a', b' y c' por s de tres rectas a, b y c del haz R^*. Según se indica en la figura 2.13, se comienza trazando cualquier circunferencia S por R y considerando las intersecciones con ella de las seis rectas dadas. Así, sean

    Ejercicio 2.10 Escríbase una macro que dé las rectas dobles para una proyectividad de un haz puntual en él mismo del cual se conocen las imágenes de tres rectas.

    Aunque aquí se ha recurrido a una circunferencia, en realidad los métodos anteriores funcionan con cualquier cónica no degenerada, ya sea elipse, hipérbola o parábola. Si en algún momento de una construcción se requiere hallar puntos dobles de una proyectividad y ya se dispone de una cónica trazada, puede aprovecharse esta misma para no complicar en exceso el dibujo.

§ 5. Polaridad inducida por una cónica

    Recordemos que dada una cónica Q en el plano, ésta induce una pareja de biyecciones, cada una inversa de la otra, entre los conjuntos de puntos y de rectas de forma que puntos alineados se transforman en rectas concurrentes y viceversa. Estas biyecciones se denominan polaridades y se denotan mediante P->P^{^} y r->r^{^}. A la recta P^{^} se la conoce como la polar del punto P, y al punto r^{^}, como el polo de la recta r. Antes de describir cómo actúan estas biyecciones, conviene refrescar las siguientes propiedades de una polaridad:

i) A perteneciente a r si y solo si r^{^} pernetece a A^{^}.

ii) Si un punto A no pertenece a la cónica y una recta r por A corta a Q en dos puntos U y V, entonces la polar A^{^} de A pasa por el cuarto armónico B de la terna (U,V,A).

iii) A perteneciente a Q si y solo si A perteneciente a A^{^}, en cuyo caso, A^{^} es la recta tangente a la cónica Q en el punto A.

iv) A = r^{^} si y solo si r = A^{^}, es decir, un punto es el polo de una recta si y solo si la recta es la polar del punto.

    Este segundo enunciado nos permite elaborar un método para el trazado de la polar de un punto no situado sobre la cónica (véase la figura 2.14). Puesto que una recta queda determinada por dos de sus puntos, bastará con trazar dos rectas por A secantes a Q que proporcionan el cuadrivértice (U,U',V,V') del que A es uno de los puntos diagonales. Ahora, como se vio en la sección § 1, resulta inmediato que la recta que pasa por los otros dos puntos diagonales P y Q contiene a los cuartos armónicos de las ternas (U,V,A) y (U',V',A) y, por consiguiente, PQ = A^{^}. Obsérvese que la combinación de las propiedades i) y iii) nos permite deducir que las intersecciones con Q de la polar A^{^} dan los puntos de tangencia (si existen) de las tangentes a la cónica por A.

    Ejercicio 2.11 Escríbase una macro que dé la polar de un punto respecto de una cónica a la cual no pertenece.

    Ejercicio 2.12 Dadas una cónica Q y un punto A fuera de Q, trácense, si existen, las tangentes a la cónica por A.

    Ahora debe ser fácil trazar polos de rectas, así como polares de puntos sobre la cónica. En efecto, si lo que deseamos es hallar el polo de una recta r, bastará con colocar dos puntos A y B sobre r y utilizar nuestra macro del ejercicio 2.11 para obtener sus respectivas polares A^{^} y B^{^}. La propiedad i) nos garantiza que el polo r^{^} buscado pertenece a ambas polares, es decir, r^{^} = A^{^}.B^{^}.

    Ejercicio 2.13 Hállese el polo de una recta respecto de una cónica dada.

    Por último, para encontrar la polar de un punto A situado sobre la cónica, o sea, la tangente a la cónica en A, trazaríamos por A una recta r y hallaríamos el polo r^{^} de r. Las propiedades i) y iii) nos permiten ahora afirmar que la recta buscada no es otra que la determinada por A y r^{^}.

    Ejercicio 2.14 Escríbase una macro que dé la tangente a una cónica en un punto de ella.

    Finalizaremos esta sección recordando el concepto de conjugación respecto de una cónica. De dos puntos A y B se dice que son conjugados respecto de una cónica Q, si la polar de uno pasa por el otro (A perteneciente a B^{^} o, equivalentemente, B perteneciente a A^{^}). Dos rectas r y s son conjugadas respecto de Q si el polo de una pertenece a la otra (r^{^} pertenece a s o S^{^} pertenece a r).

§ 6. Métodos proyectivos de construcción de cónicas

    Gracias a CABRI nos resulta sumamente fácil trazar una cónica de la que se conocen cinco puntos pues hay una herramienta preparada para ello. También hemos visto en el ejercicio 2.8 cómo hacerlo sin recurrir a ella. Sin embargo, en muchas ocasiones son otros los elementos conocidos de una cónica, dos puntos y tres tangentes o cuatro puntos y la tangente en uno de ellos, etcétera. Aquí trataremos algunos de estos casos (no todos).

    Supongamos, por ejemplo, que de una cónica Q solo se sabe que pasa por A y que las tangentes en los puntos M y N son las rectas r y s que se cortan en O (figura 2.15). Pues bien, se demuestra que si se toma un punto arbitrario P de la recta AM distinto de A y de M, y se construyen los puntos P' = OP.AN y B = MP'.NP, entonces el punto B siempre cae sobre la cónica.

    Ejercicio 2.15 Escríbase una macro que trace la cónica de la que se conocen uno de sus puntos y las tangentes en otros dos.

    Ejercicio 2.16 Constrúyase una cónica dados cuatro de sus puntos y la tangente en uno de ellos. Sugerencia: Si conocemos, por ejemplo, A, B, C y D en Q y la recta A^{^}, considerando cierta proyectividad entre los haces A^* y B^* (véase el ejercicio 2.8), podremos trazar la tangente a la cónica en B, lo que permitiría utilizar el ejercicio precedente.

    Recuérdese que las asíntotas a una hipérbola eran sus tangentes en los puntos del infinito. Este hecho nos permite aprovechar el método utilizado en el ejercicio 2.15 tomando M y N como los puntos impropios de las rectas r y s. Con tal forma de obrar, donde antes se decía recta XM, habrá que interpretar recta paralela a r por X, etcétera.

    Ejercicio 2.17 De una hipérbola se conocen las asíntotas y uno de sus puntos. Trácese la hipérbola.

    Ejercicio 2.18 Obténgase el haz de hipérbolas que tienen como asíntotas a dos rectas fijas r y s.

    Del dual del teorema de Pascal se deduce el siguiente método de obtención de tangentes a una cónica de la cual se conocen cinco tangentes p, q, r, b y c. Sea z la recta determinada por los puntos q.c y b.r. Para cada punto R perteneciente a z, constrúyanse las rectas x, y por R que pasan respectivamente por p.b y p.c. Entonces los puntos q.x y r.y determinan una nueva tangente a la cónica.

    Ejercicio 2.19 De una cónica se conocen cinco tangentes. Trácese la cónica por envolventes.

    Un resultado al que, por problemas de tiempo, no suele llegarse en los cursos universitarios de geometría proyectiva es el siguiente:

    Teorema de Sturm Las intersecciones de un haz de cónicas con una recta que no atraviese por los puntos base proporcionan parejas de puntos, eventualmente superpuestos, que se transforman uno en otro por una involución de la recta.

    Hay que aclarar algunos de los términos utilizados en el enunciado del teorema. En primer lugar el de haz de cónicas. Se trata de una imponer a una familia de cónicas la satisfacción de determinadas condiciones, las cuales requieren de ciertos ingredientes iniciales. Estos pueden ser:

i)

cuatro puntos no alineados llamados puntos base,

ii)

tres puntos no alineados (puntos base) y la tangente en uno de ellos (recta base), o

iii)

dos puntos distintos (puntos base) y dos rectas distintas que pasan por ellos (rectas base).

    Podemos visualizar con CABRI algunas de las cónicas de una familia. Por ejemplo (figura 2.16), sitúense en el tablero de trabajo cuatro puntos libres A, B, C y D, que harán de puntos base del haz, y un quinto punto E sobre una recta r. Escójase la herramienta Cónica para trazar la cónica que pasa por los cinco puntos anteriores. Bastará animar el desplazamiento de E sobre la recta r para obtener algunas de las cónicas del haz. Hay que puntualizar que incluso desplazando E a lo largo de toda la recta r no se obtiene por este método todo el haz, pues algunas de las cónicas que pasan por los puntos base no tienen intersección con la recta r. Sin embargo, el problema de acceder a la totalidad de las cónicas del haz de puntos base A, B, C y D no será tratado aquí.

    Una aplicación inmediata del teorema de Sturm consiste en el trazado de una cónica no degenerada Q conocidos cuatro de sus puntos A, B, C y D, no habiendo tres de ellos, alineados, y una de sus tangentes r. Si pudiéramos encontrar el punto de tangencia de r, el problema de trazar la cónica pedida lo tendríamos resuelto gracias al ejercicio 2.16. A eso nos dedicaremos entonces. Sígase el razonamiento que se avecina por medio de la figura 2.17. Consideremos el haz de cónicas de puntos base A, B, C y D. Sea s:r->r la proyectividad determinada por las parejas de intersecciones de r con lados opuestos del cuadrivértice, es decir, la proyectividad que aplica el punto de corte con r de la recta determinada por dos de los vértices del cuadrivértice, con la intersección con r de la recta que pasa por los dos puntos restantes del cuadrivértice. Según un conocido teorema de Desargues, s es una involución. Así, si

    Ahora bien, el teorema de Sturm predice que hay otra involución t:r->r que transforma cada intersección de r con una de las cónicas del haz en la otra intersección, y entre las cónicas del haz, están las dos cónicas degeneradas compuestas, una por el par de rectas AB y CD y la otra, por el par de rectas AD y BC. De ahí que t deba coincidir con s. ¿Qué cónicas del haz cortarán a r en un solo punto? Respuesta: aquellas que sean tangentes a r. Todas estas consideraciones nos llevan a que los puntos dobles de s darán los puntos de tangencia de la cónica buscada, por lo que habrá 0, 1 ó 2 soluciones a nuestro problema dependiendo del número de puntos dobles de s. En la figura 2.17 se han calculado los puntos dobles E y F recurriendo a una macro auxiliar que proporciona los puntos dobles de una involución. Esta macro se ha escrito utilizando las indicaciones que se dieron en la sección § 4. Una vez hallados los puntos de tangencia, CABRI nos permite trazar las cónicas correspondientes. En nuestro caso, hay dos soluciones, las dos cónicas que pasan por A, B, C y D y que son tangentes a r, la primera en E y la segunda en F.

    Ejercicio 2.20 Escríbase una macro que dibuje las posibles cónicas que pasan por cuatro puntos no alineados y son tangentes a una recta que no contiene a ninguno de esos puntos.

§ 7. Búsqueda de elementos notables en cónicas

    Recuérdese que una primera clasificación de las cónicas pasaba por dividirlas en con o sin centro. El centro de una cónica es el polo de la recta del infinito. Las cónicas no degeneradas que poseen centro son la hipérbola y la elipse, mientras que la parábola carece de centro. Las polares de puntos del infinito se conocen bajo el nombre de diámetros. Todos los diámetros pasan por el centro. Los ejes de una cónica son rectas respecto de las cuales la cónica es simétrica. La elipse y la hipérbola poseen dos ejes. La parábola, sólo uno. A las intersecciones de una cónica con sus ejes se les denominan vértices. En esta sección aprenderemos a encontrar el centro, los ejes y los vértices de cónicas no degeneradas.

    A fin de determinar el centro de una cónica (con centro), conviene repasar lo visto en la sección § 5. Se pretende hallar el polo de la recta del infinito (figura 2.18), para lo que necesitamos las polares de dos puntos impropios. Para ello, elijamos dos paralelas r y s que cortan a la cónica en el cuadrivértice (A,B,C,D). El punto del infinito de r (que es el mismo que el de s), es uno de los puntos diagonales del cuadrivértice, de ahí que su polar esté determinada por los puntos diagonales E = AB.CD y F = AC.BD. Ya tenemos un diámetro: el EF. Repitiendo el proceso con otro par de paralelas r' y s', que cortan a la cónica en un nuevo cuadrivértice (A',B',C',D'), hallaremos otro diámetro E'F', donde E' = A'B'.C'D' y F' = A'C'.B'D'. El centro O reposa en ambos diámetros.

    Ejercicio 2.21 Constrúyase una macro que proporcione el centro de una cónica (si lo tuviera) sin más que señalarla con el ratón.

    Dada una cónica Q y un punto A que pertenece a Q, en el haz de rectas A^* que pasan por A se define una aplicación s que transforma cada recta x del haz en su recta conjugada, o sea, en la determinada por A y el polo de x. Es un hecho conocido que esta aplicación s es una proyectividad. Por otro lado, no es difícil demostrar que también es una proyectividad la aplicación t:A^*->A^* que aplica cada recta del haz en su perpendicular por A.

    Ejercicio 2.22 Si nos encontramos dibujada una cónica con centro (una elipse o una hipérbola), hállense sus ejes y sus vértices. Indicación: Los ejes no serán sino las rectas dobles de la proyectividad del haz de diámetros en sí mismo que aplica cada diámetro en el perpendicular a su diámetro conjugado.

    De una parábola se conocen dos puntos A y B y el eje r (figura 2.19). Se pretende trazar la parábola. Por una lado, los respectivos simétricos A' y B' respecto de r son también puntos de la parábola. Si encontrásemos un quinto punto, por ejemplo, el vértice, el problema estaría concluido. Para ello, consideremos el cuadrivértice (en este caso, trapecio) (A,B,B',A'). Uno de los puntos diagonales de este cuadrivértice está en el infinito. A éste lo denominaremos G. A los otros dos puntos diagonales los hemos llamado E y F en la figura. En términos proyectivos, la recta EF (el eje), es la polar de G y, por consiguiente, los puntos E y F son conjugados armónicos respecto de las dos intersecciones de la cónica proyectiva con el eje. Una de estas dos intersecciones es el vértice V buscado. La otra X está en el infinito. El problema queda resuelto sin más que recordar un conocido resultado de la geometría proyectiva, aquel que afirmaba que cuando partimos de una cuaterna armónica (X,V,E,F) y llevamos a X al infinito, en la recta afín resultante el punto V queda situado justo en la mitad del segmento determinado por los puntos E y F.

    Ejercicio 2.23 Conocidos dos puntos y el eje de una parábola, trácese la parábola.

Sesión anterior	Volver a página principal	Siguiente sesión