| Volver a página principal | Siguiente capítulo |
PROBLEMAS DE ENTRENAMIENTO
|
ÍNDICE |
§ 1. Circunferencias inscritas en triángulos
El incentro de un triángulo es el centro de la circunferencia inscrita en él. Puesto que esta circunferencia se encuentra equidistante de los lados, y el lugar geométrico de los puntos equidistantes de los lados de un ángulo no es sino la bisectriz del ángulo, es evidente que el incentro habrá de encontrarse en la intersección de las bisectrices de los ángulos internos de un triángulo.
Figura 1.1
Una vez trazado el incentro, el radio de la circunferencia lo proporciona la distancia entre el centro y uno cualquiera de los lados. Dicho de otra forma, la circunferencia inscrita es tangente a los tres lados, y de ahí que los puntos de tangencia caigan sobre los respectivos pies de las perpendiculares por el centro a los lados. En la figura 1.1 las bisectrices son las rectas de color verde, mientras que la perpendicular por el centro a lado AC está dibujada en amarillo.
Pero los lados del triángulo pueden prolongarse en rectas que forman ángulos externos. Las bisectrices de estos ángulos se intersecan en centros de otras circunferencias, denominadas exinscritas, que también son tangentes a los tres lados.
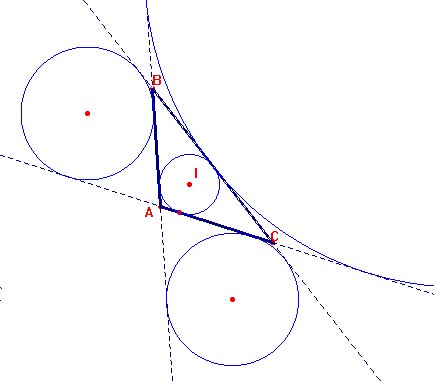
Figura 1.2
Ejercicio 1.1 Dado un triángulo, trácense la circunferencia inscrita y las tres circunferencias exinscritas.
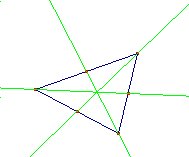
El matemático del renacimiento italiano L. Fagnano, se planteó el siguiente problema: Dado un triángulo de vértices A, B y C, encuéntrese el triángulo inscrito en él de menor perímetro.
Puede demostrarse que la solución la proporciona el triángulo integrado por los pies de las perpendiculares por cada vértice a sus respectivos lados opuestos. Este triángulo, dibujado en rojo en la figura 1.2, se denomina triángulo órtico.
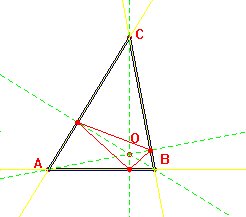 |
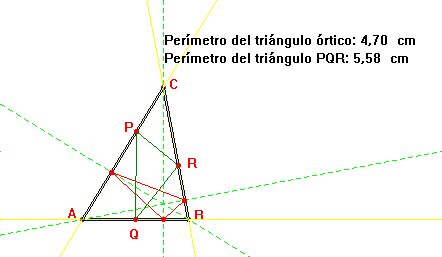 |
|
|
|
Ejercicio 1.2 Compruébese experimentalmente la corrección de la solución al problema de Fagnano.
§ 3. Ejercicio sobre rotaciones
Aquí se pretende construir un triángulo equilátero con sus vértices situados en tres rectas paralelas.
Figura 1.5
Obsérvese en la figura 1.5, que si se considera el problema resuelto, una rotación s de 60o alrededor del vértice A, llevaría B a C, de donde C no es sino la intersección con t de la imagen h = s(s) de la recta s.
Ejercicio 1.3 Dadas tres paralelas, dibújese un triángulo equilátero con un vértice en cada una de ellas.
§ 4. Más puntos notables en triángulos
El circuncentro es el centro de la circunferencia circunscrita a un triángulo. Es, por consiguiente, equidistante de los vértices, por lo que habrá de situarse en la confluencia de las tres mediatrices a los lados.
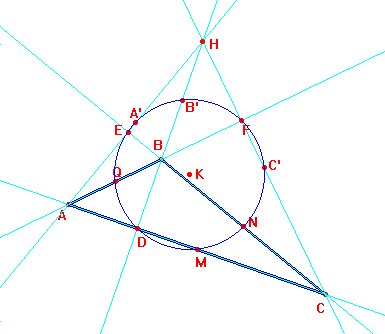
El baricentro es el punto donde concurren las tres medianas. Proporciona el centro de gravedad de un triángulo. En las figuras 1.6 y 1.7 se encuentran las respectivas construcciones del circuncentro y el baricentro de un triángulo.
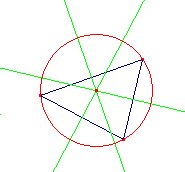 |
 |
|
|
|
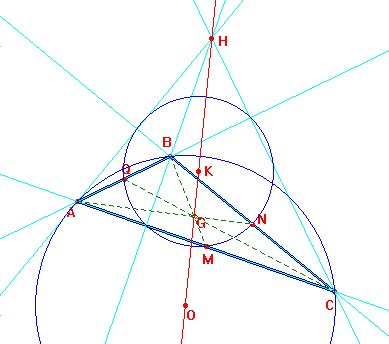
Ejercicio 1.4 Compruébese experimentalmente la validez del siguiente teorema: Sean ABC un triángulo, M, N y Q los puntos medios de los lados, D, E y F los pies de las alturas, H el ortocentro (punto de intersección de las alturas), y A', B' y C' los puntos medios de los segmentos AH, BH y CH. Entonces, los nueve puntos D, E, F, M, N, Q, A', B' y C' reposan todos en la misma circunferencia, denominada la circunferencia de los nueve puntos. Además, si K es el centro de la circunferencia de los nueve puntos, O es el circuncentro y G es el baricentro, entonces O, G, H y K pertenecen a una recta conocida como recta de Euler.
 |
 |
|
|
|
§ 5. Trazado de una cónica por envolventes
Es un hecho conocido que si se recorta un círculo en papel, se señala un punto P en su interior y se elige otro punto Q sobre la circunferencia, al flexionar la hoja para hacer coincidir P sobre Q, el doblez que se forma (recta en verde en la figura 1.10), resulta ser una tangente a cierta elipse. De esa forma, tomando tantos puntos en el borde como se desee, trazaríamos la elipse envolvente a ese haz de rectas.
Figura 1.10
Ejercicio 1.5 Constrúyase un mecanismo CABRI que reproduzca la construcción de una elipse como envolvente de un haz de rectas descrita más arriba. Experiméntese con distintas posiciones para el punto P, en el exterior de la circunferencia, en el interior o sobre ella.
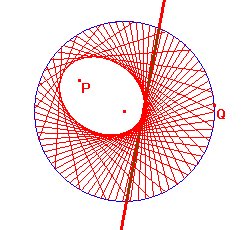
Figura 1.11
Supongamos que se numeran consecutivamente los vértices de un polígono Qn de n lados. Se considera el simétrico Q(1) de Qn respecto del vértice 1. A continuación, el simétrico Q(2) de Q(1) respecto de la imagen del vértice 2 por la primera simetría. Y así sucesivamente. En la figura 1.12 se ha construido esa serie de polígonos con CABRI, hallando un resultado curioso, uno de los Q(m) coincide con el polígono de partida. Sin embargo, no siempre sucede así.
Figura 1.12
Ejercicio 1.6 Ofrézcanse distintos ejemplos de polígonos Qn para los cuales se obtengan los dos tipos de resultado posibles, y elabórese alguna conjetura sobre el particular.
Al pedir el enunciado de una conjetura, nos referimos a que después de experimentar con distintos polígonos, quizás uno se atrevería a extraer de sus observaciones una hipótesis del tipo: algún Q(m) coincide con el primitivo Qn si al polígono Qn le sucede tal puñetería.
Dados una circunferencia de centro O y un punto U, se define la cardioide, o caracol de Pascal, como el lugar geométrico de las intersecciones de las tangentes a la circunferencia por Q con paralelas al diámetro OQ por U.
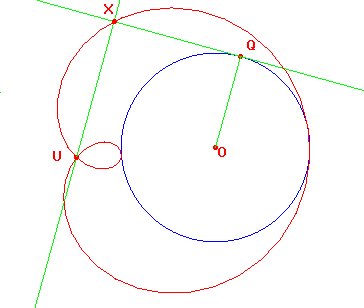
Figura 1.13
Ejercicio 1.7 Constrúyase una cardioide y experiméntese con distintos radios y posiciones relativas entre U y la circunferencia.
Un punto R se desplaza por la tangente a una circunferencia en el punto S. Llamemos A al antípoda de S. (Véase la figura 1.14.) Cualquier segmento AR corta a la circunferencia en otro punto Q distinto de A. Pues bien, el punto P del segmento AR cuya distancia a A coincide con la distancia entre Q y R describe una curva denominada la cisoide de Diocles.
Matemáticos como Fermat, Huygens o Newton estudiaron la cisoide. Este último incluso ideó un mecanismo para su trazado. En los ejercicios teóricos de este tema se verá que con una cisoide trazada es posible resolver el histórico problema de la duplicación del cubo.
Figura 1.14
No es difícil probar que si la circunferencia tiene radio a, está centrada en el punto de coordenadas (a,0) y la tangente tiene de ecuación x = 2a, entonces la cisoide queda descrita por una ecuación del tipo
|
Ejercicio 1.8 Elabórese un mecanismo en CABRI que dibuje una cisoide.
Ejercicio 1.9Dibújese con CABRI una bandera ajedrezada como la de la figura 1.15, y dótesela de movimiento haciendo que uno de los vértices se desplace sobre una circunferencia oculta.
Figura 1.15
| Volver a página principal | Siguiente capítulo |